Выполнение расчетов с накоплением. Сумма

Перевод
Выполнение расчетов с накоплением. Сумма

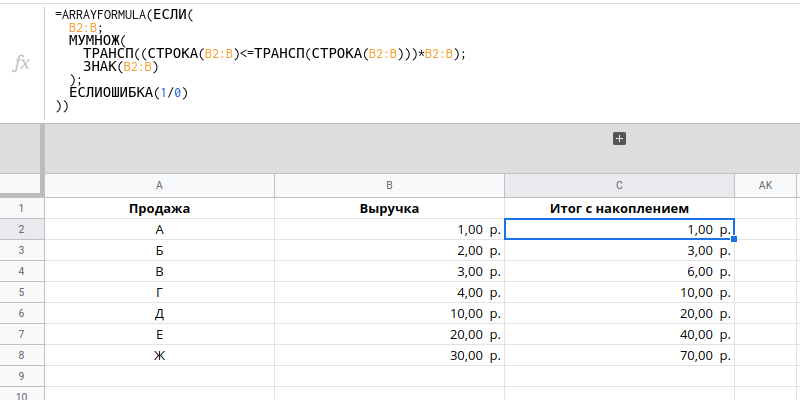
Выполнение расчетов с накоплением в Google Sheets с использованием формул массива.

Перевод “Running Total Array Formulas (using the MMULT function) ”.

В этой статье мы рассмотрим, как вычислить промежуточную сумму, используя стандартный метод и метод формулы массива. Мы рассмотрим тему умножения матриц (сделайте глубокий вдох, все будет хорошо!), используя формулу MMULT, одну из самых экзотических и сложных формул в Google Sheets.

Это урок из моего последнего курса Google Sheets по программе Advanced Formulas 30 Day Challenge (это бесплатно!).

В следующих примерах мы будем использовать этот набор данных:

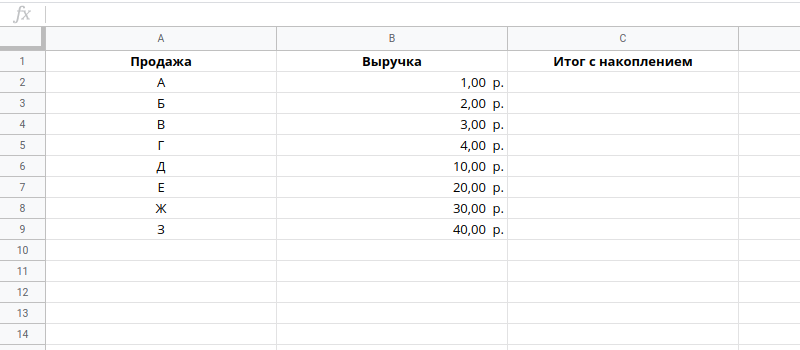
набор данных для промежуточного итога

Мы хотим добавить промежуточную сумму в столбце C.

Давайте начнем с самого простого метода, используя стандартную (не массивную) формулу, которую мы затем можем скопировать в наш столбец.

Взяв приведенный выше набор данных, мы запускаем итоговую сумму в ячейке C2 по следующей формуле:

= B2

Она просто возвращает наше первое значение, которое является единственным значением на данном этапе.

Для нашего второго значения и далее мы можем использовать ту же стандартную формулу, просто добавляя новое значение к промежуточной сумме из строки выше:

= B3 + C2

Затем эту формулу можно “протянуть” для всех строк вниз до необходимого значения, чтобы получить промежуточный итог:

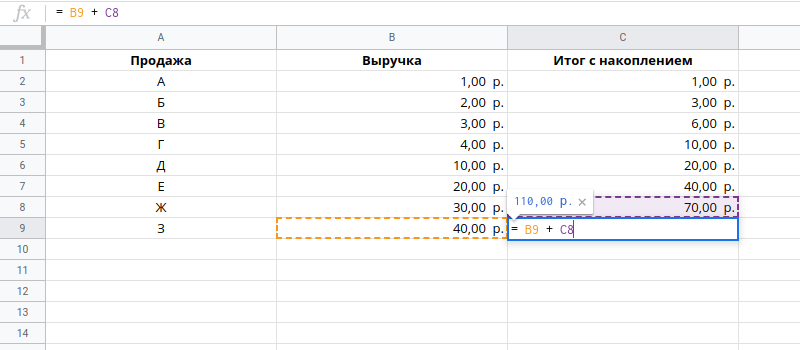
простая формула формула промежуточного итога

Если в набор данных добавляются новые элементы, эту формулу необходимо будет “протянуть” для всех строк вниз. Или вы можете предварительно заполнить столбец, протянув его до конца таблицы и добавляя оператор IF, чтобы скрыть пустые строки, например:

=IF(ISBLANK(B3), "", B3 + C2)

Основным недостатком этой формулы является необходимость заполнения всего столбца новой формулой для каждой строки.

Было бы неплохо, если бы мы могли иметь единственную формулу в верхней части столбца для расчета промежуточного итога, верно?

Но сначала …

Прошло много времени с тех пор, когда я изучал умножение матриц, поэтому я выкопал одну из моих книг по математике для выпускников “[Sets & Groups, A First Course in Algebra]” автор J.A. Green.

Как только я преодолел первоначальный шок, увидев надпись “Ben Collins 1999”, написанную на внутренней стороне обложки (да, я действительно такой старый!), я перешел на страницу 192 и вспомнил старые добрые времена… нет, я имею в виду, что обновился мой взгляд на особенности матриц, особенно их умножение.

Единственное определение, которое стоит упомянуть здесь, относящееся к функции MMULT, это следующее:

Произведение AB матриц A = (aij) и B = (bhk) определяется тогда и только тогда, когда число столбцов в A равно числу строк в B.

Другими словами, если A имеет размерность (m, n), то B должена иметь размерность (n, p), чтобы это работало. Полученная матрица будет иметь размерность (m, p).

Каждая запись в новой матрице определяется правилом

(i, k) элемент AB = i строка A * k столбец B

Формула MMULT делает это матричное умножение за нас. Она принимает матрицы A и B в качестве аргументов = MMULT (A, B) и выводит матричное произведение AB.

Фух, хватит уже о математике, давайте вернемся к более комфортной области - к нашей Таблице.

Теперь вы знаете, как выполнять умножение матриц, давайте использовать это в примере с функцией MMULT.

Давайте выработаем стратегию, прежде чем погрузиться с головой в формулы, и отметим, что:

  1. Матрица в одну строку, 1 x N, умноженная на матрицу из одного столбца совместимого размера, N x 1, приведет к матрице размером 1 x 1, то есть к единственному значению.

  2. Далее, если дана матрица строк {a, b, c} и матрица столбцов {x; y; z}, то их произведение будет ax + by + cz, одно значение, равное сумме перемноженных элементов.

  3. Итак, если мы сможем получить значения из нашего диапазона в столбце B в формате строки и умножить их на вектор столбца, мы сможем сложить их!

  4. Трюк состоит в том, чтобы создать матрицу 1, которая имеет только “правильные” значения в каждой строке, поэтому для строки 1 она должна иметь только первое значение, для строки 2 - первые два, для строки 3 - первые три и т. д. Т.е. только текущие или предыдущие значения в каждой строке нашей матрицы.

  5. Матрица 2 просто позволяет выполнять умножение, чтобы можно было добавлять значения. Таким образом, для этого будет достаточно 1 вектора.

Возвращаясь к рассматриваемой проблеме, используя набор данных, представленный в верхней части этого поста, давайте начнем с построения двух матриц для нашей функции MMULT. Я рекомендую ограничить диапазон до B2:B10, чтобы обеспечить управляемость вычислений, пока мы анализируем формулу. Как только у нас будет рабочая формула, мы можем открыть диапазон до B2:B.

Начните с этой формулы в ячейке E2:

=ARRAYFORMULA(ROW(B2:B10))

который просто дает нам вектор-столбец чисел от 2 до 10, то есть {2; 3; 4; 5; 6; 7; 8; 9; 10}

Добавьте эту формулу в ячейку F1:

=ARRAYFORMULA(TRANSPOSE(ROW(B2:B10)))

который просто транспонирует вектор столбца выше в вектор строки чисел, то есть {2,3,4,5,6,7,8,9,10}

Теперь давайте создадим матрицу 9 x 9, сравнив эти два вектора и записав, является ли значение из вектора столбца меньше или равно значению из вектора строки, используя:

=ARRAYFORMULA(ROW(B2:B10) <= TRANSPOSE(ROW(B2:B10)))

Теперь у нас должен быть следующий вывод (добавлено цветовое обозначение):

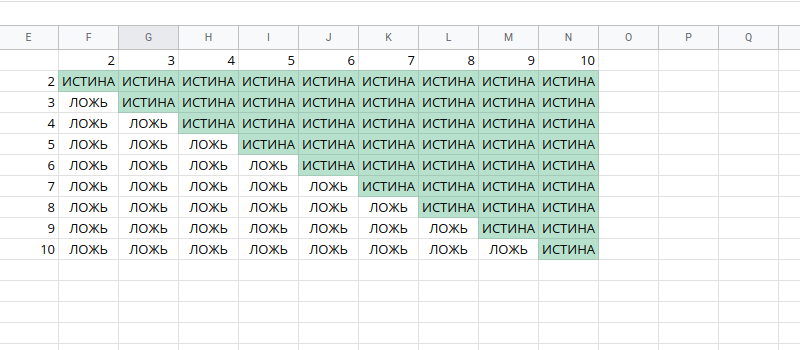
строка и столбецб векторная матрица

что дает ИСТИНА, где значение вектора столбца меньше или равно значению вектора строки, и ЛОЖЬ в противном случае.

Умножая это на исходный диапазон данных, B2:B10, вы превращаете ИСТИННЫЕ значения в числа, а ЛОЖНЫЕ - в нули:

=ARRAYFORMULA((ROW(B2:B10) <= TRANSPOSE(ROW(B2:B10)))*B2:B10)

где мы применяем функцию транспонирования, чтобы перевернуть данные в подходящую ориентацию

=ARRAYFORMULA(TRANSPOSE((ROW(B2:B10) <= TRANSPOSE(ROW(B2:B10)))*B2:B10))

так что значения из нашего диапазона данных в B2:B10 теперь располагаются в формате 9 на 9, правильно начинаясь с соответствующей строки (поэтому значение в B2 начинается со строки 2, значение в B3 начинается со строки 3 и т. д.), как показано на этом изображении:

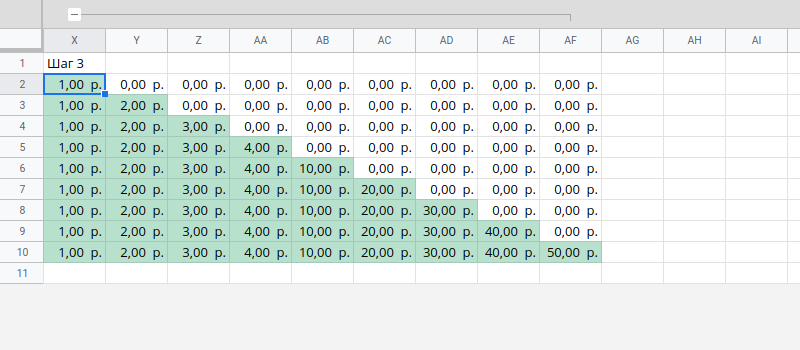
google Таблицы. РАсчет с накоплением

Итак, первая матрица готова для формулы MMULT.

Давайте построим вторую матрицу. К счастью, это немного проще:

=ARRAYFORMULA(SIGN(B2:B10))

который создает матрицу 9 на 1 или вектор столбца, где любые положительные числа в диапазоне B2:B10 возвращают 1, а пустые ячейки возвращают 0, поэтому конечным результатом является вектор нашего столбца {1; 1; 1; 1; 1; 1; 1; 1; 1}. Удалим пару нижних строк для наглядности. Конечный вектор нашего столбца на текущий момент {1; 1; 1; 1; 1; 1; 1; 0; 0}

Добавьте оба массива как аргументы функции MMULT и наблюдайте волшебство:

=ARRAYFORMULA(MMULT(
  TRANSPOSE((ROW(B2:B10) <= TRANSPOSE(ROW(B2:B10)))*B2:B10),SIGN(B2:B10)
))

Напомним, что после умножения матриц матрица 9 на 9, умноженная на матрицу 9 на 1, приводит к новой матрице 9 на 1.

Each element in the first row of matrix 1 is multiplied by the column values in matrix 2, and added together, which if I try to illustrate, looks like this: Каждый элемент в первой строке первой матрицы умножается на значения столбцов во второй матрице 2 и все складывается вместе. Я попытаюсь проиллюстрировать, выглядит следующим образом:

Первый ряд первой матрицы 1 равен {1\0\0\0\0\0\0\0\0}

Первая колонка второй матрицы {1;1;1;1;1;1;1;0;0}

Первая строка расчета:

1*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*0 + 0*0
= 1 + 0 + 0 + 0 + 0 + 0 + 0 + 0 + 0
= 1

(Возможно, вы заметили, что это матрица 1 на 9, умноженная на матрицу 9 на 1, что приводит к матрице 1 на 1 или просто к одному значению)

Соответственно, вторая строка расчета:

1*1 + 2*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*0 + 0*0
= 1 + 2 + 0 + 0 + 0 + 0 + 0 + 0 + 0
= 3

Третья:

1*1 + 2*1 + 3*1 + 0*1 + 0*1 + 0*1 + 0*1 + 0*0 + 0\*0
= 1 + 2 + 3 + 0 + 0 + 0 + 0 + 0 + 0
= 6

И так далее, к нашему желаемому результату:

{1\3\6\10\20\40\70\70\70}

Таким образом, эта формула дает промежуточный итог.

Последний шаг - показывать значения только в непустых строках, чего мы добиваемся стандартной логикой IF.

Здесь я использовал следующую конструкцию

IFERROR(1/0)

чтобы гарантировать, что ячейки пустые, когда диапазон B2:B10 пуст. 1/0 всегда приводит к #DIV/0! ошибке, поэтому обертка IFERROR оставляет ячейку пустой.

Итак, наша формула сейчас:

=ARRAYFORMULA(IF(
  B2:B10;
  MMULT(
    TRANSPOSE((ROW(B2:B10)<=TRANSPOSE(ROW(B2:B10)))*B2:B10);
    SIGN(B2:B10)
  );
  IFERROR(1/0)
))

который можно обобщить весь столбец B, удалив ссылку на 10 строк из B2:B10.

Наша формула в своем конечном состоянии:

=ARRAYFORMULA(IF(
  B2:B;
  MMULT(
    TRANSPOSE((ROW(B2:B)<=TRANSPOSE(ROW(B2:B)))*B2:B);
    SIGN(B2:B)
  );
  IFERROR(1/0)
))

как показано на следующем рисунке:

google Таблицы. ARRAYFORMULA, MMULT. Расчет с накоплением

Если новые строки данных добавляются в столбцы A и B, столбец промежуточного итога будет обновляться автоматически.

Пример Таблицы

Да, попробуйте сами , пожалуйста.

Бонус: расчет итогов промежуточных итогов одной формулой

Это просто проыверка идеи.

Можно создать единую формулу массива, которая создает отдельные промежуточные суммы для каждого уникального элемента в столбце A, до 9 уникальных элементов, как показано на следующем рисунке:

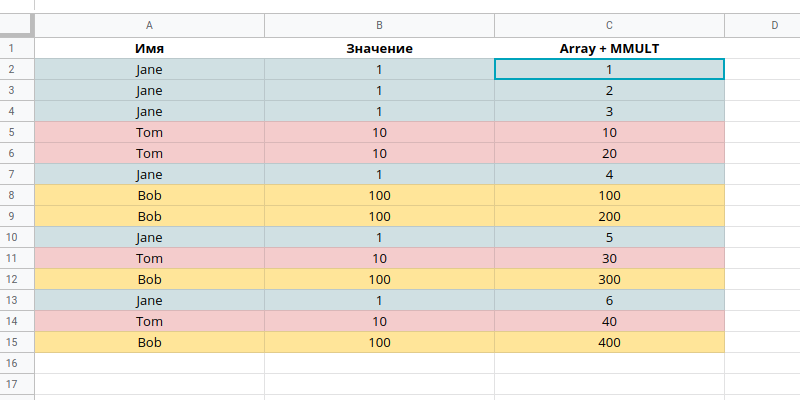
google Таблицы. Расчет с накоплением и группировкой

Формула для этого - полный зверь (и я не говорю, что это единственный или лучший способ достижения этого):

=ARRAYFORMULA(QUERY(
  QUERY(
    IF(
      {TRANSPOSE(UNIQUE(INDIRECT("A6:A"&COUNTA($A$2:$A)+1)))}=$A$2:$A;
      MMULT(
        TRANSPOSE((ROW($B$2:$B)<=TRANSPOSE(ROW($B$2:$B)))*$B$2:$B);
        IF({TRANSPOSE(UNIQUE(INDIRECT("A6:A"&COUNTA($A$2:$A)+1)))}=$A$2:$A;1;0)
      );
      0
    );
    "select "&
      LEFT(
        CONCATENATE(TRANSPOSE("Col"&ROW(INDIRECT("1:"&COUNTUNIQUE($A$2:$A)))&"+"));
        COUNTUNIQUE($A$2:$A)*5-1
      )&
        " label "&
          LEFT(
            CONCATENATE(TRANSPOSE("Col"&ROW(INDIRECT("1:"&COUNTUNIQUE($A$2:$A)))&"+"));
            COUNTUNIQUE($A$2:$A)*5-1
          )&
            " ''";
     0);
  "select * limit "&counta(A2:A)
))

Само собой разумеется, я не собираюсь разбивать это построчно, по крайней мере, не сегодня.

Если вам интересно, лучший способ приблизиться к cсуть того, как это работает - это очистить слои (как лук), пока вы не достигнете самой внутренней формулы, а затем собрать всё обратно.

Удачи!