Выполнение расчетов с накоплением. Произведение
Вероятно, суммой с накоплением уже удивить кого-то сложно. Однако, из этой формулы можно вывести произведение с накоплением. Если вспомнить курс школьной метематики.
Постановка задачи
Посчитать произведение с накоплением. Что-то вроде: даны числа 1, 2, 3, требуется посчитать 1, 1*2, 1*2*3 и т.п.
![Произведение с накоплением]
Формула для тех, кто все уже знает
Хм… не в этот раз ;)
При чем тут математика
Решение базируется на предыдущей статье “Выполнение расчетов с накоплением. Сумма ”. Из нее вы можете узнать, как построить формулу, и как она работает.
Самым важным в этом вопросе, является свойство логарифмов:
Сумма логарифмов с одинаковыми основаниями равна логарифму произведения выражений, стоящих под знаками логарифмов слагаемых:
ln(x) + ln(y) = ln(xy), (x>0, y>0).
![Свойство суммы логарифмов]
Обновление формулы
Предыдущая формула расчитывала суммы с накопительным итогом. Как ее вывести написано в статье
![Расчет с накоплением суммы]
=ARRAYFORMULA(IF(
B2:B;
MMULT(
TRANSPOSE((ROW(B2:B)<=TRANSPOSE(ROW(B2:B)))*B2:B);
SIGN(B2:B)
);
IFERROR(1/0)
))
Из упомянутого математического свойства логарифмов мы можем вытянуть, что e^(ln(x)+ln(y)) = e^ln(xy) = xy, (x>0, y>0). Отлично, то что надо! Видимо, нам нужно получить натуральный логарифм всех наших значений, сложить их, получить значение, а потом возвести экспоненту в степень, равную полученному значению. Да проще паренной репы:
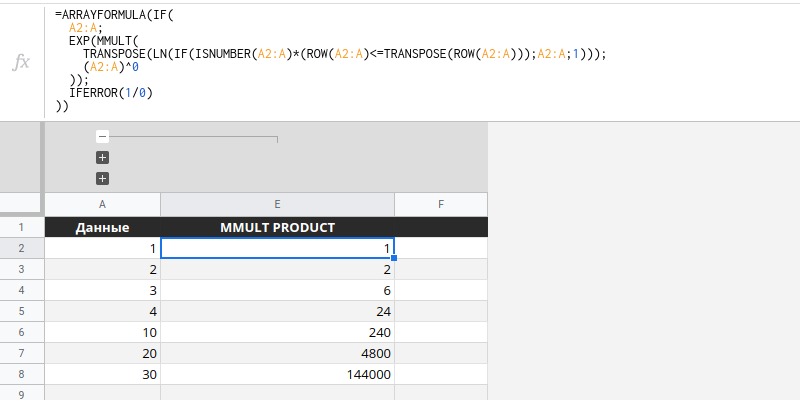
![Расчет с накоплением произведения MMULT]
=ARRAYFORMULA(IF(
A2:A;
EXP(MMULT(
TRANSPOSE(
LN(IF(ISNUMBER(A2:A)*(ROW(A2:A)<=TRANSPOSE(ROW(A2:A)));A2:A;1))
);
(A2:A)^0
));
IFERROR(1/0)
))
Особенности формулы с MMULT
Произведение и степень требуют к себе тщательного подхода, а значит, нам требуется проверять значение на число ISNUMBER(A2:A).
Другой, уже “неприятной”, особенностью является требование использовать только положительные значения. Иной формулы пока нет.
Преимуществом этой формулы является ее невероятная мощность и легкость в производстве. Она почти не потребляет расчетное время, и может работать с огромным массивом.
Альтернатива
Альтернативной формулой в данном варианте выступает QUERY. Еще бы! Я буду ссылаться уже на другую предыдущую статью “QUERY. Большое число колонок
”. В данном случае, нам потребуется расчитать не агрегатную функцию, а обычное произведение всех колонок. Вот так
![Соединение запроса QUERY с SEQUENCE]
А следовательно
![Расчет с накоплением произведения QUERY]
=ARRAYFORMULA(QUERY(
TRANSPOSE(
(ROW(A2:A10)<=TRANSPOSE(ROW(A2:A10)))*A2:A10 +
(ROW(A2:A10)>TRANSPOSE(ROW(A2:A10)))
);
"select Col" & JOIN("*Col";SEQUENCE(1;ROWS(A2:A10)));
))
Особенности формулы с QUERY
Эта формула тоже не без изъяна. Она очень тяжелая и “падает” при большом числе строк. Например, при 1000 строк уже не каждый ПК “потянет” её.
Преимущество в том, что она считает отрицательные числа. Считает правильно.
А еще она требует правки заголовков, т.к. QUERY без заголовков не бывает ;-) Пример обрезки
![Расчет с накоплением произведения QUERY без заголовков]
=ARRAYFORMULA(QUERY(
TRANSPOSE(
(ROW(A2:A10)<=TRANSPOSE(ROW(A2:A10)))*A2:A10+
(ROW(A2:A10)>TRANSPOSE(ROW(A2:A10)))
);
"select Col" & JOIN("*Col";SEQUENCE(1;ROWS(A2:A10)))&
" label Col" & JOIN("*Col";SEQUENCE(1;ROWS(A2:A10)))&"''";
))
Уверен, что найдется решение для любого числа и типа данных. Будем пробовать.
Ссылки
- Примеры в Таблице . Можно сделать копию [Произведение с накоплением]: /img/post/google-sheets-running-product-calculations_01.png [Свойство суммы логарифмов]: /img/post/google-sheets-running-product-calculations_02.png [Расчет с накоплением суммы]: /img/post/google-sheets-running-product-calculations_03.png [Расчет с накоплением произведения]: /img/post/google-sheets-running-product-calculations_04.png [Соединение запроса QUERY с SEQUENCE]: /img/post/google-sheets-running-product-calculations_05.png [Расчет с накоплением произведения QUERY]: /img/post/google-sheets-running-product-calculations_06.png [Расчет с накоплением произведения QUERY без заголовков]: /img/post/google-sheets-running-product-calculations_07.png